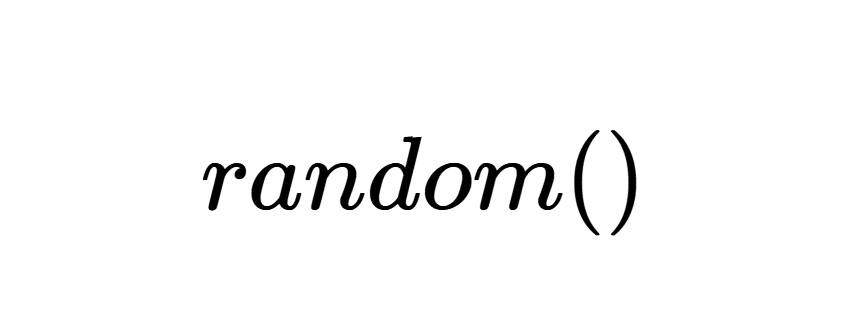Connue pour la présence quasi systématique des probabilités, l’épreuve de Maths II fait toujours intervenir des questions de programmation Python. Ceci vaut également pour les épreuves Ecricome, EDHEC et Emlyon. Il convient donc de maîtriser parfaitement la simulation de l’aléatoire en Python pour être prêt le jour J.
Introduction
Pour simuler l’aléatoire en Python, il est nécessaire d’importer la librairie qui contient les codes usuels afin de pouvoir simuler les lois de variables aléatoires usuelles. Ainsi, avant chaque programme simulant de l’aléatoire, il est absolument nécessaire de le faire précéder de la ligne de code qui permet d’importer la librairie numpy.random : import numpy.random as rd.
Que tu sois en première année de prépa ECG ou en deuxième année, cet article pourra t’aider puisqu’il sera question non seulement de la simulation des variables aléatoires discrètes (généralement vue en première année), mais également de la simulation des variables aléatoires à densité (vue en deuxième année généralement).
L’aléatoire en Python est-il réellement aléatoire ?
Voici là une question que l’on peut se poser : l’aléatoire a-t-il sa place dans un langage de programmation déterminé ? Voici comment fonctionne la commande \(rd.random()\) afin de comprendre le fonctionnement de l’aléatoire en Python. Pour rappel, la commande \(rd.random()\) est censé renvoyer un nombre aléatoire compris entre 0 et 1.
En réalité, Python mobilise une fonction (notée « f ») au comportement le plus « chaotique » et construit avec elle une suite \((x_n)_{n\in
\mathbb{N}}\) définie par \(x_{n+1} = f(x_n)\). L’objectif est que pour des grandes valeurs de \(n\), la valeur de \(x_n\) soit la plus aléatoire possible. À partir d’une certaine valeur suffisamment aléatoire de \(x_n\), on définit une fonction g qui à \(x_n\) associe un réel de \([0,1]\). On parle alors de génération pseudo-aléatoire. Ainsi, la commande \(rd.random()\) ne renvoie pas réellement un réel de \([0,1]\) aléatoire, mais suffisamment hasardeux pour que l’on considère qu’il est presque aléatoire.
Ceci dit, passons en revue les différentes façons de simuler l’aléatoire en Python en passant en revue les manières de procéder avec les lois usuelles (discrètes puis à densité).
Simulation des variables aléatoires discrètes
La loi uniforme discrète
La commande \(rd.randint(n)\) permet de renvoyer un entier compris entre \(1\) et \(n-1\) de manière aléatoire. Attention donc au décalage d’indice dans le programme Python. Si l’on veut simuler la variable aléatoire \(U \hookrightarrow
\mathcal{U}([\![1,n]\!])\), on aura le code suivant :
Plus encore, il est possible de généraliser la formule pour \(U \hookrightarrow
\mathcal{U}([\![a,b]\!])\) où \( (a,b) \in
\mathbb{Z^2} , b\ge a\). En effet, la commande \(rd.randint(a,b)\) renvoi un entier aléatoire compris entre \(a\) et \(b-1\). On aura donc le code suivant, et de la même manière, il faut faire attention au décalage d’indice :
La loi binomiale
Pour cette loi, on dispose directement d’un code présent dans la librairie numpy.random. Si on a \(B \hookrightarrow
\mathcal{B}(n,p)\), alors le code pour simuler \(B\) sera le suivant :
Rien de compliqué donc pour cette loi !
La loi de Bernoulli
Il existe deux manières de simuler une loi de Bernoulli de paramètre \(p\) où \(p \in [0,1]\) .
Première possibilité : approche par la loi binomiale
Une première méthode consiste à considérer qu’une loi de Bernoulli n’est qu’une loi binomiale où l’on répète une même expérience aléatoire de Bernoulli une seule fois. On a donc \(n=1\) et on simule alors la loi binomiale comme nous l’avons vu précédemment en remplaçant \(n\) par \(1\) dans le code précédent.
Deuxième possibilité : retour aux bases (if/else)
Il est également possible avec « if » et « else » de renvoyer l’entier \(1\) avec une probabilité \(p\) et un entier \(0\) avec une probabilité \(1-p\). Ici, on prend un élément de \( [0,1]\). Or la probabilité que \(u\) soit supérieur à \(p\) vaut exactement \(p\) puisque on a \( (u,p) \in
[0,1]^2 \). On a donc :
La loi géométrique
Comme pour la loi binomiale, on dispose d’un code dans la librairie numpy.random pour simuler une réalisation d’une loi géométrique de paramètre \(p\). On a :
La loi de Poisson
De la même manière, on a pour la loi de Poisson (ici de paramètre \(L\)) le code suivant qui permet de simuler la réalisation d’une variable aléatoire suivant une telle loi :
Simulation des variables aléatoires à densité
La loi uniforme à densité
Soit \(U \hookrightarrow \mathcal{U}([0,1])\), alors on simule U avec l’instruction \(rd.random()\). Assez simple dans le cas d’une loi uniforme dans \([0,1]\) mais comment procéder dans le cas général si \(U \hookrightarrow
\mathcal{U}([a,b])\)où \( (a,b) \in
\mathbb{Z^2} , b\ge a\)?
Retour au cours sur les transformées affines de lois uniformes à densité ! Pour rappel, si \(U \hookrightarrow \mathcal{U}([0,1])\), alors \(Y = a + (b-a)U \hookrightarrow \mathcal{U}([a,b])\). Dès lors, voici le code pour simuler une loi uniforme à densité dans le cas général :
La loi exponentielle
Soit \( a>0\), alors l’instruction \(rd.exponential (1/a)\) permet de simuler la loi exponentielle de paramètre \(a\). Attention donc à bien mettre la fraction dans le code !
La loi gamma
Il y a deux possibilités pour la loi gamma, soit l’utilisation d’une instruction directement prévue dans la librairie numpy.random, soit on ruse avec le cours !
Première possibilité : recours direct à la librairie numpy.random
Soit \( a>0\), alors l’instruction \(rd.gamma (a)\) permet de simuler la loi exponentielle de paramètre \(a\). Le code est donc le suivant :
Deuxième possibilité : recours à la loi exponentielle
Il est également possible de simuler une loi gamma de paramètre \(\ n \in
\mathbb{N^{*}}\) avec des lois exponentielles de paramètre \(1\). Puisque \(X \hookrightarrow
\mathcal{E}(1) \Leftrightarrow X \hookrightarrow
\gamma(1)\) et par théorème de stabilité de la loi gamma pour des variables indépendantes, on a :
\( Y = \displaystyle \sum_{i=1}^{n}X_i \hookrightarrow
\gamma(n) \) où \(X_i \hookrightarrow
\mathcal{E}(1)\)
On aura donc le code suivant (qui fait appel aux vecteurs aléatoires vus un peu plus tard dans cet article !) :
La loi normale
Là encore, deux méthodes sont possibles et les deux sont bonnes à connaître !
Première possibilité : cas général simple
Soit \(X \hookrightarrow\mathcal{N}(\mu,\sigma^2)\), alors le code suivant permet de simuler X :
Attention, dans l’instruction \(rd.normal(… , …)\), on remplit seulement \(\sigma\) alors que l’on simule pour \(\sigma^2\).
Deuxième possibilité : la loi normale centrée réduite
Mais il est également possible de simuler toute loi normale à partir d’une transformée de la loi normale centrée réduite d’après le cours. En effet, si \(X \hookrightarrow
\mathcal{N}(0,1)\), alors \(X^{*} = \sigma X + m \hookrightarrow\mathcal{N}(\mu,\sigma^2)\). On a donc le code suivant qui permet de simuler \(X^{*}\) :
Vecteurs aléatoires
Pour simuler l’aléatoire en Python, il est également parfois nécessaire de recourir à des vecteurs aléatoires, c’est-à-dire la simulation aléatoire d’une même loi usuelle un grand nombre de fois dans un seul et même vecteur.
Pour la plupart des lois usuelles, il suffit de rajouter une virgule dans l’instruction de la loi en rajoutant le nombre voulu de répétitions. Note que les vecteurs contiendront des réalisations indépendantes de la loi en question.
Par exemple, pour simuler n-lois uniformes indépendantes de paramètres \(a\) et \(b\), le code sera le suivant :
Voici les autres possibilités réunies dans la même page de code. On a la loi binomiale (ligne 1), la loi géométrique (ligne 3), la loi de Poisson (ligne 5), la loi uniforme à densité (ligne 7), la loi exponentielle (ligne 9), la loi gamma (ligne 11) et la loi normale (ligne 13) (on note m la taille du vecteur) :
Comment dès lors faire pour simuler \(n\)-réalisations d’une loi uniforme à densité de paramètres \(a\) et \(b\) ? On simule un vecteur pour une loi uniforme à densité de paramètres \(0\) et \(1\) et on multiplie chaque élément de ce vecteur par \((b-a)\), puis on rajoute a (cf. simulation d’une loi uniforme de paramètres \(a\) et \(b\)). On a donc le code suivant :
Il est également possible de réaliser des matrices de réalisations de même loi en Python. Cela fonctionne de la même manière que pour la création de vecteurs, sauf qu’il faut indiquer cette fois-ci entre crochets le nombre de lignes et de colonnes et non plus seulement le nombre de réalisations.
Exemple : pour réaliser une matrice de taille \(n\times p\) de réalisations indépendantes d’une loi uniforme de paramètres \(a\) et \(b\), on aura :
Simulation de quelques lois aléatoires non usuelles
Loi du min/loi du max
Soit \(n \in\mathbb{N^{*}}\), on pose alors la variable aléatoire \(U\) définie par \( U = min (X_1,…,X_n)\) où tous les \(X_i\) suivent la même loi et sont indépendantes (hypothèse très importante). Il est possible en Python de simuler la réalisation d’une telle variable aléatoire en faisant appel aux vecteurs aléatoires. Ce cas tombe très souvent aux concours, le sujet Maths II 2024 en est une belle illustration !
Exemple : supposons que \(\forall i \in [\!
[1,n]\!], X_i \hookrightarrow
\mathcal{N}(\mu,
\sigma^2)\), alors le code qui simulera une réalisation de \(U\) sera le suivant :
On a ici développé l’exemple de la loi du minimum de \(n\)-variables aléatoires, mais cela fonctionne exactement de la même manière pour le maximum, il suffit simplement de remplacer \(min\) par \(max\) dans le code Python ci-dessus.
Transformées de loi normale
Il est également possible à partir de ces lois usuelles de simuler toute loi pouvant s’exprimer comme transformée de lois usuelles. Prenons deux exemples classiques qui reviennent très souvent aux concours : la loi de Rayleigh et la loi du Khi 2. Pour comprendre en quoi ces deux lois sont des transformées de loi normale (notion hors programme), tu peux lire cet article.
Loi de Rayleigh
Soient \(X_1 , X_2\) deux variables aléatoires indépendantes suivant toutes les deux une loi normale de paramètres \(0\) et \(\sigma^2 \), alors la variable aléatoire définie par \(Z = \sqrt{X_1^2 + X_2^2}\) suit la loi de Rayleigh de paramètre \(\sigma\).
Pour réaliser une réalisation de la loi de Rayleigh, on peut donc proposer le programme Python suivant :
Loi du Khi 2
Soient \(n\) variables aléatoires \(X_1,…,X_n\) indépendantes suivant une loi normale centrée réduite, alors \( X=\displaystyle \sum_{k=1}^{n}{X_k}^2\) suit la loi du Khi 2 à \(n\) degrés de liberté.
À partir de cette expression, on peut donc simuler une réalisation de la loi du Khi 2 à \(n\) degrés de liberté :
Nous avons donc ici vu l’exemple de deux lois ultraclassiques qui s’avèrent être des transformées de la loi normale. De la même manière, il est en fait possible en Python de simuler des réalisations de toute variable aléatoire en fonction de variables aléatoires usuelles.
Conclusion
En définitive, la librairie numpy.random est très riche et permet de réaliser des réalisations d’un très grand nombre de lois usuelles (discrètes et à densité). Il est également possible de réaliser des programmes plus complexes faisant appel à des vecteurs ou à des matrices aléatoires. Et plus généralement, il est possible de simuler une réalisation de toute loi qui peut s’écrire comme une transformée de lois usuelles.
Face à cette grande diversité au sein de la librairie numpy.random , il est essentiel de s’entraîner sur ces notions pour être à l’aise le jour J. Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !